The Ulam Spiral is a famous cool thing. See Wikipedia Entry. Basically, Ulam put numbers on a square spiral and colored the prime numbers black.
 |
 |
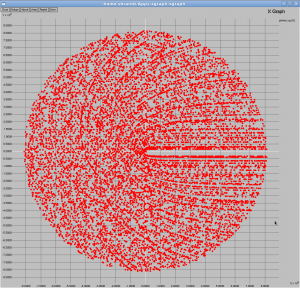
One variant of it is to plot an Archemedean Spiral instead, that is you let r = theta = some constant * sqrt(prime). Plot all the primes as black dots. If you pick 8*pi as your value for “some constant” you get this image:
It took some fiddling to find a good image. Pick the wrong constant and you just get a bunch of random dots. This particular plot shows a nice empty patch along the X-axis and it leads to the following conjecture:
For any number p, let a = 8*pi*sqrt(p). If abs(a*sin(a)) < 10e-4 and a*cos(a) > 54, then p is not prime.
I can’t prove this in general, but it’s true for the first million primes.